


Next: Semi-noyau et sous-espace semi-hilbertien
Up: Présentation Spline vectorielle à
Previous: Formulation mathématique
Après avoir vérifié l'existence et l'unicité d'une solution
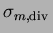 et
et
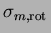 ,
on applique la théorie des semi-noyaux de Schwartz aux espaces
,
on applique la théorie des semi-noyaux de Schwartz aux espaces
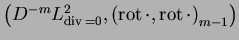 et
et
 pour caractériser de manière simple ces solutions.
pour caractériser de manière simple ces solutions.
2001-02-17