Théorème 4 (Caractérisation : divergence nulle)
Soit
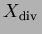
le tenseur défini en (
2).
Alors la solution
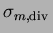
du problème
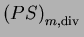
est de la forme
où
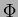
est une mesure orthogonale à
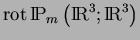
,
de la forme
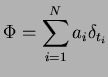
(les
N
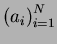
sont des éléments de
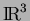
)
et
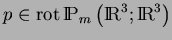
.
Les contraintes d'interpolation
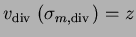
et les conditions d'orthogonalité définissent de façon unique le polynôme
p et le vecteur
a.
Théorème 5 (Caractérisation : rotationnel nul)
Soit
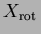
le tenseur défini en (
1).
Alors, la solution
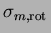
du problème
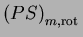
est de la forme
où
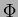
est une mesure orthogonale à
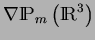
,
de la forme
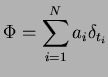
(les
N
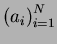
sont des éléments de
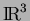
)
et
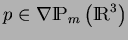
.
Les contraintes d'interpolation
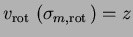
et les conditions d'orthogonalité définissent de façon unique le polynôme
p et le vecteur
a.
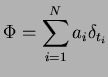 (les N
(les N
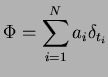 (les N
(les N
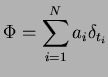 (les N
(les N