An antenna in the direction 
, placed at some point in
the focal plane and illuminating the telescope produces a radiation
field propagating in the direction 
in the sky:
where 
is the field amplitude produced by the antenna, while
and
are conventional basis vectors forming a right handed
orthogonal reference frame with the direction of propagation . The
only property of these vectors that we use, is that they turn by an angle
around
if the antenna, and therefore
, is rotated by this angle in the focal plane. The
Ludwig III convention is an example satisfying this constraint. If
the antenna is rotated by an angle of 
toward the direction Y,
the basis vector in the far field reference frame are rotated in the same
way:
the field produced in the same direction
in the sky becomes:
In other words an emitter in the focal plane illuminating the
telescope with a field 
, produces in the direction a
radiation field 
given by:
where the (
) reference frame in the focal plane is defined by the
two orthogonal directions of the antenna.
The principle of reciprocity
tells us that an incoming radiation field in the
direction
, produces in the focal plane a field
Therefore,
by illuminating the telescope in the reverse way with two orthogonal
dipoles in the focal plane, and studying their antenna patterns, one
is able to evaluate the full polarised lobe as a Jones matrix
depending on the direction of an incoming radiation.
Note that with the matrix in Eq. (18), one is able to
compute the Jones matrix in any other reference frame
(
), rotated by an angle from (X,Y) in the focal
plane, provided the Co-Cross reference frame chosen for the incoming
radiation also rotates by the same angle :
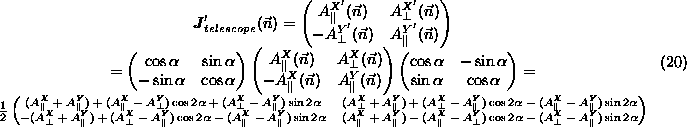
The first and second lines
of this matrix give the Co and Cross amplitudes relative to the
and 
directions respectively.
The action of a polarimeter placed behind, at an
angle
from the X axis, is obtained as the product 
, where 
is given by the expression
(13). If, as argued by Fosalba [Fosalba2000], the copolar
amplitude depend only very weakly on the direction of the dipole in
the focal plane, and the crosspolar amplitudes are small, then the
Jones matrix is approximately:
When working with bolometers, Mueller matrices are more illuminating,
as they give directly the transformation of the Stokes parameters.
The Mueller matrix associated to the Jones matrix (21) is,
to first order in 
and 
and assuming that the induced
circular polarisation is negligible (The Jones matrix is nearly real):
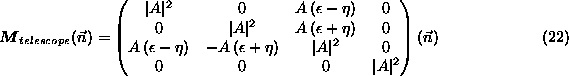
Multiplying by the Mueller matrix of the polarimeter (Eq.
14), one finds the coefficients:
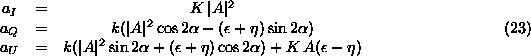
where 
and 
If and are zero, then one is back to equation
(17), up to a factor 
which is the transmission of the
telescope. The whole instrument behaves as a polarimeter in the direction
in the focal plane. If and are small but not
zero, the angle is changed to 
and
gets a small contribution, proportional to 
.
Still, the result of Fosalba [Fosalba2000] should be checked for all feed positions and is probably a bad approximation for far side-lobes. Therefore we think that the polarised beams as complete Jones matrices (four complex amplitudes up to a phase) should be evaluated for each feed, thus allowing to play with the polariser directions and to choose the optimal ones.