


Next: {`A} propos de ce
Up: Applications numériques
Previous: Spline d'interpolation à divergence
Afin de mettre en évidence l'intérêt des splines à rotationnel nul, nous avons interpolé le champ vectoriel f à rotationnel nul et défini par
On interpole avec 31 points répartis aléatoirement sur la grille
![$[-\pi,\pi]^3$](img68.png) (figure 4).
La figure 5 représente le champ f en la coupe
(figure 4).
La figure 5 représente le champ f en la coupe
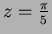 Les figures 7 et 6 représentent, respectivement, le champ spline `` plaque-mince '' 2-harmonique et le champ spline à rotationnel nul
Les figures 7 et 6 représentent, respectivement, le champ spline `` plaque-mince '' 2-harmonique et le champ spline à rotationnel nul
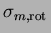 .
Commentaires
Il est à remarquer que le champ f n'est pas défini en
.
Commentaires
Il est à remarquer que le champ f n'est pas défini en
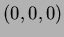 .
Nous obtenons de meilleurs résultats en utilisant la spline
.
Nous obtenons de meilleurs résultats en utilisant la spline
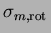 .
En effet, on peut remarquer que la source au point
.
En effet, on peut remarquer que la source au point
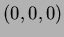 et les puits aux points
et les puits aux points
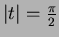 sont bien plus prononcés sur la figure 6 relative à la spline à rotationnel nul que sur la figure 7. La spline `` plaque-mince '' 2-harmonique est beaucoup plus influencée par la répartition des données.
sont bien plus prononcés sur la figure 6 relative à la spline à rotationnel nul que sur la figure 7. La spline `` plaque-mince '' 2-harmonique est beaucoup plus influencée par la répartition des données.
Figure 4:
Repartition aléatoire de 31 points
Figure:
Champ
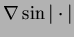 théorique à rotationnel nul
théorique à rotationnel nul
|
|
Figure:
Champ
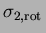 avec 31 données interpolant
avec 31 données interpolant
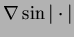
Figure:
Champ
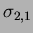 avec 31 données interpolant
avec 31 données interpolant
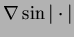
|
|



Next: {`A} propos de ce
Up: Applications numériques
Previous: Spline d'interpolation à divergence
2001-02-17