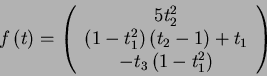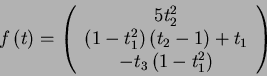Next: Spline d'interpolation à rotationnel
Up: Applications numériques
Previous: Applications numériques
Nous nous proposons d'interpoler le champ à divergence nulle f défini par
On interpole avec
 points régulièrement répartis sur la grille
points régulièrement répartis sur la grille
![$[-1,3]\times[-1,1]^2$](img58.png) .
La figure 1 représente la coupe en t3=0 du champ f. Les points d'interpolation appartenant à cette coupe sont représentés par des étoiles. Les courbes fines sont différentes lignes de courant de ce champ. La courbe épaisse est la seule ligne de courant calculée en un point appartenant aux points d'interpolation. Les figures 2 et 3 représentent respectivement la coupe en t3=0, des champs f,
.
La figure 1 représente la coupe en t3=0 du champ f. Les points d'interpolation appartenant à cette coupe sont représentés par des étoiles. Les courbes fines sont différentes lignes de courant de ce champ. La courbe épaisse est la seule ligne de courant calculée en un point appartenant aux points d'interpolation. Les figures 2 et 3 représentent respectivement la coupe en t3=0, des champs f,
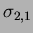 ainsi que certaines lignes de courant.
Toutes les lignes de courant sont calculées par rapport aux mêmes points de départ.
Commentaires
Si l'on regarde globalement ces trois figures sans les lignes de courant, il nous semble que la spline `` plaque-mince '' (figure 2) donne de bons résultats. Seule une étude plus fine (représentation graphique plus locale pour éviter la mise à l'échelle due à quiver3 nous permet de constater qu'il n'en est rien.
En particulier, nous obtenons de très mauvais résultats si on regarde les lignes de courant qui sont très différentes de celle du champ théorique f. Seule la ligne de courant évaluée au point d'interpolation
ainsi que certaines lignes de courant.
Toutes les lignes de courant sont calculées par rapport aux mêmes points de départ.
Commentaires
Si l'on regarde globalement ces trois figures sans les lignes de courant, il nous semble que la spline `` plaque-mince '' (figure 2) donne de bons résultats. Seule une étude plus fine (représentation graphique plus locale pour éviter la mise à l'échelle due à quiver3 nous permet de constater qu'il n'en est rien.
En particulier, nous obtenons de très mauvais résultats si on regarde les lignes de courant qui sont très différentes de celle du champ théorique f. Seule la ligne de courant évaluée au point d'interpolation
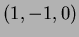 (figure 2) est acceptable bien qu'elle passe par le point
(figure 2) est acceptable bien qu'elle passe par le point
 : la ligne de courant du champ théorique passe quand à elle par le point
: la ligne de courant du champ théorique passe quand à elle par le point
 (figure 1).
La spline
(figure 1).
La spline
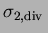 (figure 3) donne de bien meilleurs résultats et ceci avec très peu de points d'interpolation (45 points sur
(figure 3) donne de bien meilleurs résultats et ceci avec très peu de points d'interpolation (45 points sur
![$[-1,3]\times[-1,1]^2$](img58.png) ). La ligne de courant évaluée en un point d'interpolation donne de très bons résultats. On passe par le point
). La ligne de courant évaluée en un point d'interpolation donne de très bons résultats. On passe par le point
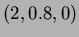 qui est très proche du point
qui est très proche du point
 (figure 1).
(figure 1).
Figure 1:
Champ f théorique à divergence nulle
Figure:
Champ
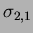 avec 45 données interpolant f
avec 45 données interpolant f
|
|
Figure:
Champ
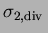 avec 45 données interpolant f
avec 45 données interpolant f
|
|



Next: Spline d'interpolation à rotationnel
Up: Applications numériques
Previous: Applications numériques
2001-02-17