Waves in thin disks
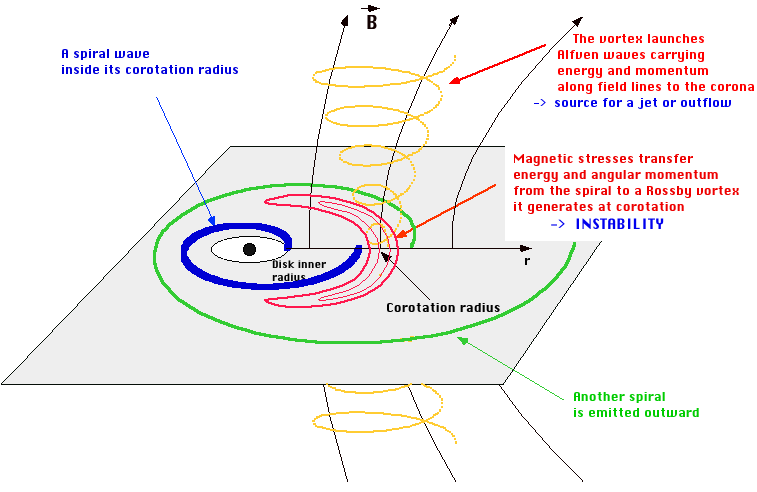
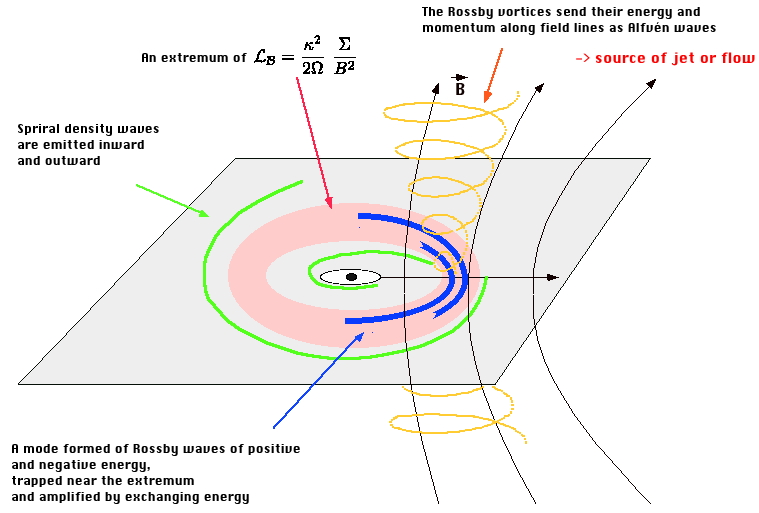
Spiral density waves are in fact ordinary sound waves, i.e. compressional perturbations that propagate in the disk, modified by the various effects that distinguish it from an ordinary fluid: differential rotation, the epicyclic force, Lorentz force, self-gravity, and the thin-disk geometry (the disk height is smaller than the typical wavelengths, giving behaviors similar to waves in shallow water).But disks also admit Rossby waves: these are well known in planetary atmospheres, where they propagate perturbations of vorticity (the Great Red Spot of Jupiter can be viewed as an extreme non-linear form of Rossby waves). In accretion disks, density waves and Rossby waves are coupled by differential rotation, exchanging energy and angular momentum: a density wave can spawn a Rossby wave, and vice-versa. Thus in the Accretion-Ejection Instability (AEI) a spiral density wave extracts energy and angular momentum from the inner region of the disk (this causes accretion of the gas) and stores them in a Rossby wave near its corotation radius (the radius where the wave rotates at the same angular velocity as the gas), and in this process the spiral may be amplified, making the AEI an instability. This mechanism also acts in self-gravitating disks (for galactic spirals) and in disks where the sole force comes from the gas pressure, although in these cases it is usually stabilizing.
This is where the magnetic field introduces a major difference, besides making the AEI unstable: the Rossby wave represents a twisting motion that is applied to the footpoints of magnetic field lines threading the disk, and in magnetized plasmas such a twisting will in turn propagate along the field lines - this is the nature of Alfven waves. Thus the magnetic stresses allows a significant fraction of the accretion energy and angular momentum, extracted from the disk, to be re-emitted upward to the corona as Alfvén waves: this explains the "E" in "AEI", since it turns accretion into a possible source of energy for jets.
Global modes
Global modes can be analyzed as standing patterns established as waves, which rotate in the disk at a given frequency w, travel radially back and forth between reflection points. In galaxies, a spiral wave traveling inward is reflected at the center as an outgoing wave. In an unmagnetized accretion disk around a black hole, the gas reaching the inner edge of the disk (the Marginally Stable Orbit, or MSO) forms a "plunging region" toward the black hole, and waves are not expected to be reflected there.On the other hand various reasons of theoretical or observational origin, summed up in the mechanism we have called "Magnetic Floods", have lead us to consider the fate of the vertical magnetic flux advected with the gas, as it flows toward the black hole. This magnetic flux must get trapped between the black hole and the disk, and be contained by a current ring at the inner edge of the disk. No theoretical or numerical model has yet been able to describe this configuration, in General Relativistic MHD, when the inner region of the disk is fully magnetized (i.e. the magnetic pressure is of the order of equipartition with the gas pressure), and when a strong magnetic flux has accumulated around the black hole. We believe that it should be able to efficiently reflect waves.
Spiral waves are characterized by their frequency,
,
and their azimuthal wavenumber, 
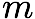(the
number of
arms of the spiral pattern, i.e.
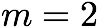in most
galactic
spirals). It can be shown that they do not propagate in the region of
their corotation radius, where their angular phase velocity,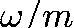 
, is
equal to the rotation frequency of the gas, W.
When a wave traveling toward corotation reaches this region it is
reflected toward the center of the disk.
1) Accretion-Ejection Instability:Thus a standing wave pattern can be established between the inner edge of the disk and the corotation region, as is classical in such cavities (e.g. waveguides, the Solar interior...). This requires an integral phase condition to be fulfilled, selecting a discrete set of frequencies.The following figure describes the basic features of the AEI: it is formed of a standing spiral pattern between the inner disk edge and corotation, a standing Rossby vortex near corotation, a spiral wave emitted outward beyond corotation, and Alfvén waves emitted from the Rossby vortex. This qualitative analysis is of course confirmed by exact, analytical and numerical, derivations in our papers. |
 |
 |
2) Rossby-Wave Instability:If the inner edge of
the
disk ddoes not
reflect waves, another form of global modes can exist if the radial
profiles of density, magnetic field, rotation frequency, etc. create an
extremum of a certain quantity in the disk (we will not describe this
quantity here, but this is similar to the constraint for the
hydrodynamical Kelvin-Helmholtz instabiliy). This can be created by an
extremum of density or magnetic field, but it also occurs naturally,
because of the relativistic rotation curve, just outside the Marginally
Stable Orbit. Rossby waves can be trapped in this extremum and also establish a standing pattern. The resulting Rossby-Wave Instability was studied in hydrodynamical disks by Lovelace and his coworkers. We find it much more unstable in magnetized disks, and have used this to explain, in particular, the quasi-periodicity observed during the flares of Saggitarius A*, the black hole at the center of the Galaxy. |