Présentation

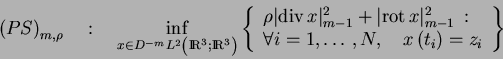
Dans le document précédent, nous avons caractérisé l'unique solution du problème de minimisation suivant :

$$\left(PS\right)_{m,\rho}\quad :\quad \inf_{x\in D^{-m}L^2\lef... ...i=1,\ldots,N,\quad x\left(t_i\right)=z_i \end{array} \right\}$$

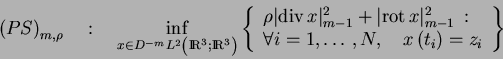
De par la forme de la semi-norme utilisée dans ce problème, il est naturel de considérer deux nouveaux problèmes de minimisation dans les sous-espaces $D^{-m}L^2_{{\mathrm{div\,}}=0}$ et $D^{-m}L^2_{{\mathrm{rot\,}}=0}$ de $D^{-m}L^2\left({\rm I\!R}^3;{\rm I\!R}^3\right)$ définis par

$$D^{-m}L^2_{{\mathrm{div\,}}=0}=\left\{x\in D^{-m}L^2\left({\r... ...!R}^3;{\rm I\!R}^3\right)\: \vert\: {\mathrm{div\,}}x=0\right\}$$

$$D^{-m}L^2_{{\mathrm{rot\,}}=0}=\left\{x\in D^{-m}L^2\left({\r... ...!R}^3;{\rm I\!R}^3\right)\: \vert\: {\mathrm{rot\,}}x=0\right\}$$

Il est à remarquer que la minimisation de $\rho\vert{\mathrm{div\,}}\cdot\vert^2_{m-1}+\vert{\mathrm{rot\,}}\cdot\vert^2_{m-1}$ (sous contraintes linéaires) dans ces deux derniers espaces peut présenter un grand intérêt dans la mesure où leurs solutions respectives seront des champs vectoriels à divergence ou rotationnel nul, préoccupation nécessaire dans de nombreux problèmes physiques.