Introduction and notation
The following formalism and notation is based on the paper by A. Lewis, (Phys. Rev. D., 71, 083008, (2005), hereafter Lewis05).
The field of a spin, ![]() , defined on a sphere (
, defined on a sphere (![]() ) is represented as,
) is represented as,
| (1) |
Both positive and negative spins are accepted by the routines. However, for the negative
spin, ![]() , we first make use of the fact that
, we first make use of the fact that
| (2) |
| (3) |
Consequently, in the following equations we will always assume that spin is non-negative
(![]() ).
).
The routines compute or use the electric (![]() ) and magnetic (
) and magnetic (![]() )
representation of the harmonic space coefficients (Lewis05). These are defined as,
(e.g., Eqs. (A4) of Lewis05),
)
representation of the harmonic space coefficients (Lewis05). These are defined as,
(e.g., Eqs. (A4) of Lewis05),
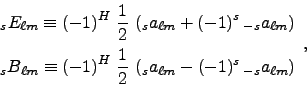 |
(4) |
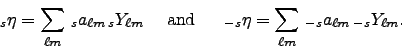
The parameter
The complex map produced or proccesed by the spin tranform routines, alm2map_spin and map2alm_spin, as two real maps, which for spin s=2 correspond to the Stokes Q an U parameter maps.
Top of the page
Spin transforms
We first define (Lewis05, Eq. (A6)),
| (5) | |||
| (6) |
-
Direct transforms:
The direct transform spin routine computes the following expressions:-
for the Northern Hemisphere,
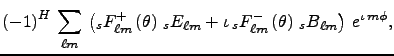
(7) 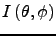
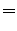
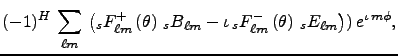
(8)
-
for the Southern Hemisphere,
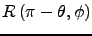
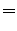
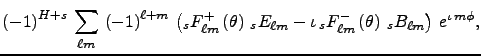
(9) 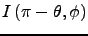
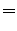
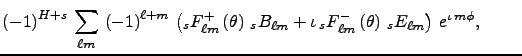
(10)
If requested spin is negative, the imaginary part of the field is subsequently multiplied by
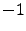 .
.
-
for the Northern Hemisphere,
-
Inverse transforms:
The inverse transform implement the following expressions:-
Electric component:
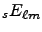
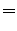
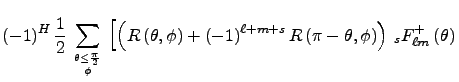

![$\displaystyle \left.
\iota\,(-1)^H\,\left(I\left(\theta, \phi\right) - (-1)^{\e...
...(\pi - \theta, \phi\right)\right)\,
_sF^{-}_{\ell m}\left(\theta\right)
\right]$](tex/spinAlgebra2html/img32.png)
(11)
-
Magnetic component:
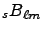
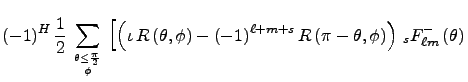

![$\displaystyle \left.
(-1)^H\,\left(I\left(\theta, \phi\right) + (-1)^{\ell+m+s}...
...\pi - \theta, \phi\right)\right)
\,_sF^{+}_{\ell m}\left(\theta\right)
\right].$](tex/spinAlgebra2html/img35.png)
(12)
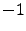 prior to the
transform calculations.
prior to the
transform calculations.
-
Electric component:
Top of the page