Introduction & notation
The core of the formalism implemented for the (un)polarized transforms is inherited from the relevant HEALpix routines, the notation of which was originally based on the paper by M. Kamionkowski, A. Kosowsky, & A. Stebbins, (Phys. Rev. D., 71, 083008, (1998), hereafter KKS98).
The polarized routines compute or use as an input, (map2alm and alm2map routines, respectively)
the total intensity scalar harmonic coefficients, ![]() , and, optionally
if requested, the electric (
, and, optionally
if requested, the electric (![]() ) and magnetic (
) and magnetic (![]() )
representation of the polarized harmonic coefficients (Lewis05), where hereafter for shortness we drop the subscript
)
representation of the polarized harmonic coefficients (Lewis05), where hereafter for shortness we drop the subscript
![]() . Those are defined as, (e.g., Eqs. (A4) of Lewis05),
. Those are defined as, (e.g., Eqs. (A4) of Lewis05),
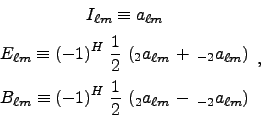 |
(1) |
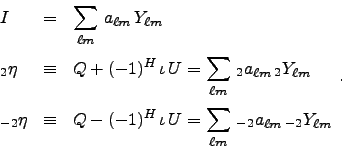
The parameter
The polarized routines process or compute maps of I, Q, and U.
Top of the page
The transforms
-
Direct transforms:
The direct transform spin routine computes the following expressions:-
for the Northern Hemisphere,
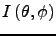
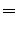
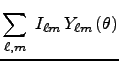
(4) 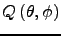
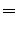
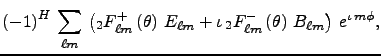
(5) 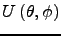
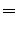
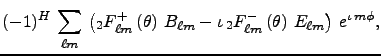
(6)
-
for the Southern Hemisphere,
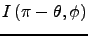
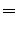
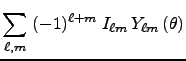
(7) 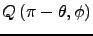
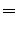
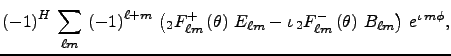
(8) 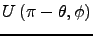
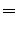
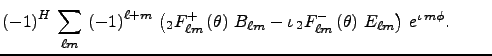
(9)
-
for the Northern Hemisphere,
-
Inverse transforms:
The inverse transform implement the following expressions:-
Scalar (total intensity) component:
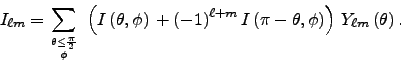
(10) -
Electric component:
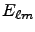
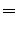
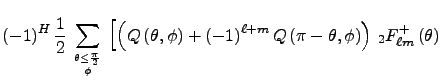

![$\displaystyle \left.
\iota\,(-1)^H\,\left(U\left(\theta, \phi\right) - (-1)^{\e...
...(\pi - \theta, \phi\right)\right)
\,_2F^{-}_{\ell m}\left(\theta\right)
\right]$](tex/polAlgebra2html/img27.png)
(11)
-
Magnetic component:
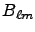
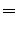
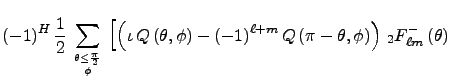

![$\displaystyle \left.
(-1)^H\,\left(U\left(\theta, \phi\right) + (-1)^{\ell+m}\,...
...\pi - \theta, \phi\right)\right)
\,_2F^{+}_{\ell m}\left(\theta\right)
\right].$](tex/polAlgebra2html/img30.png)
(12)
-
Scalar (total intensity) component:
We first define (KKS98, Lewis05, Eq. (A6)),
| (2) | |||
| (3) |
Top of the page
Next: Spin harmonics Up: Algebraic Background
radek stompor 2009-10-15