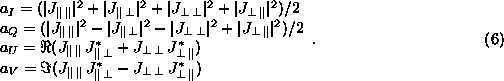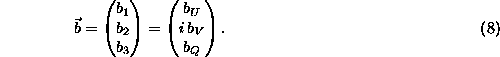Next: The Mueller matrix
Up: Description of the instrument
Previous: Description of the instrument
An instrument transforms linearly
the 2 dimensional vector representing the incoming radiation field
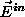 into the outgoing field
into the outgoing field 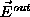 , also a 2 dimensional
complex vector. Therefore, the action of the instrument can in
general be
represented by a
, also a 2 dimensional
complex vector. Therefore, the action of the instrument can in
general be
represented by a 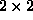 complex Jones matrix
complex Jones matrix
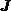 [Jones1941a, Jones1941b, Jones1942]:
[Jones1941a, Jones1941b, Jones1942]:
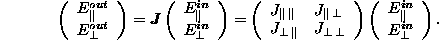
The Jones matrix depends on 7 parameters plus one irrelevant phase.
If the instrument can be split into successive parts, through which
the radiation travels before it reaches the bolometer, then the total
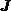 matrix is the product of the
matrix is the product of the 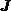 matrices of the parts. For
instance if the radiation goes first through the telescope, then through
a first horn, then through a polariser and finally through a second horn,
the total
matrices of the parts. For
instance if the radiation goes first through the telescope, then through
a first horn, then through a polariser and finally through a second horn,
the total 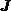 matrix of the instrument is:
matrix of the instrument is:
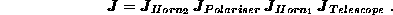
If the
Stokes parameters of the incoming radiation are 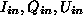 and
and 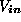 , a bolometer behind the instrument receives an intensity:
, a bolometer behind the instrument receives an intensity:
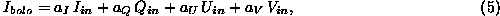
where
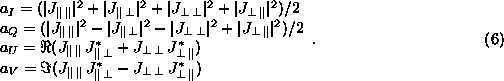
Amplitudes 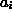 satisfy the inequality:
satisfy the inequality:
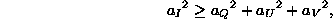
which again expresses the
fact that the instrument does not induce a polarised energy
larger than the total energy.
The
Jones matrix in terms of Pauli matrices: It is sometimes convenient to
write the
Jones matrix in terms of the Pauli matrices:

where
a can be taken real and 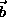 is a complex vector. To keep
track of
the reality properties of the Jones matrix, which are related to the
circular polarisation induced by the instrument, we write
the components of
is a complex vector. To keep
track of
the reality properties of the Jones matrix, which are related to the
circular polarisation induced by the instrument, we write
the components of 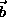 in terms of 3 parameters
in terms of 3 parameters 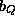 ,
, 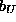 and
and
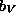 which are real when the Jones matrix is:
which are real when the Jones matrix is:
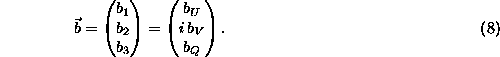
Then the Jones matrix
writes:
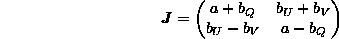
Note on the reference systems: Of course, the Jones matrix
depends on the ``in'' and ``out'' reference systems which are in
general
different. For instance the ``in'' reference system is some
conventional
``Co-Cross'' reference system orthogonal to the direction of
propagation of
the incoming radiation, whereas the ``out'' reference system lies in
the
focal plane ``Co(
``Co(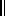 ), (Cross(
), (Cross(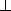 ))'' directions being parallel (orthogonal) to
the presumed direction of the polarizer.
))'' directions being parallel (orthogonal) to
the presumed direction of the polarizer.
Transformation of the coherence matrix by the instrument:
By going through the instrument, the coherence matrix 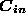 of
radiation
is transformed to:
of
radiation
is transformed to:





Next: The Mueller matrix
Up: Description of the instrument
Previous: Description of the instrument
Jean Kaplan
Wed Sep 19 13:04:59 CEST 2001