General comments:
ALGORITHM
- as usual the direct and inverse transforms are performed into two steps corresponding to the transform over azimuthal (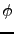 ) and polar (
) and polar (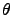 ) directions. In the memory distributed case and for the direct
transform, i.e., from a map to
) directions. In the memory distributed case and for the direct
transform, i.e., from a map to 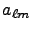 coefficients, first the
coefficients, first the 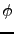 transform is performed on all the pixel rings assigned to a given proc,
while on the second step the
transform is performed on all the pixel rings assigned to a given proc,
while on the second step the 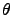 transform is computed for a set
of
transform is computed for a set
of 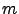 values over all rings in the map. The two steps are separated
by a global memory communication instance which redistributes
the data accordingly. The relevant routine is called: mpi_map2alm_memdist.
values over all rings in the map. The two steps are separated
by a global memory communication instance which redistributes
the data accordingly. The relevant routine is called: mpi_map2alm_memdist.
In the case of the inverse transform the two steps are performed in an inverse order as implemented in the routine: mpi_alm2map_memdist.
DATA DISTRIBUTION
- all the major data objects (i.e., those with the size of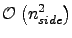 or bigger) which need to be stored in the memory
of the computer are distributed over all the processors.
That applies to maps,
or bigger) which need to be stored in the memory
of the computer are distributed over all the processors.
That applies to maps, 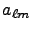 coefficients and precomputed
coefficients and precomputed
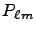 s. A submap assigned to each of the procs must not be empty
and has to contain a full number of rings. It is thus always defined by
the first and last ring, first_ring and last_ring respectively, (both of which are included in the submap). Moreover the
consecutive submaps should be assigned to the consecutive
processors.
A subset of the
s. A submap assigned to each of the procs must not be empty
and has to contain a full number of rings. It is thus always defined by
the first and last ring, first_ring and last_ring respectively, (both of which are included in the submap). Moreover the
consecutive submaps should be assigned to the consecutive
processors.
A subset of the 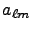 coefficients assigned to any proc
should include all the coefficients for a defined set of
coefficients assigned to any proc
should include all the coefficients for a defined set of 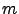 values.
Those values are arbitrary and stored on the input of all the routines
in a vector mvals of nmvals.
The precomputed
values.
Those values are arbitrary and stored on the input of all the routines
in a vector mvals of nmvals.
The precomputed 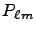 s are divided into subsets as
s are divided into subsets as 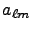 and using the same sets of
and using the same sets of 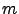 values though they are computed for
all rings of the map. The routines: get_local_data_ sizes,
distribute_map, distribute_w8ring, distribute_alms,
collect_map,
values though they are computed for
all rings of the map. The routines: get_local_data_ sizes,
distribute_map, distribute_w8ring, distribute_alms,
collect_map, collect_alms, collect_cl precompute the "load-balanced" distribution of the data or distribute and collect the data from or to a selected processor. MEMORY REQUIREMENTS
- for the load balanced distribution of the maps and the alm coefficients the rough memory requirement is:- maps -
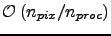 with a prefactor of the order of few;
with a prefactor of the order of few;
- alms -
![${\cal O}\left[\left(\ell_{max}+1\right)\left(m_{max}+1\right)/2/n_{procs}\right]$](img8.png) with a prefactor around 1;
with a prefactor around 1;
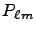 s
is dominated by the storage of the precomputed data values. The total
memory required to store all the precomputed data is
s
is dominated by the storage of the precomputed data values. The total
memory required to store all the precomputed data is
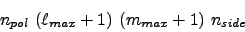
of doubles (8bytes), where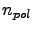 is
either 1 for scalar and 3 for all precomputed
is
either 1 for scalar and 3 for all precomputed 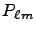 s. For standard choices of
s. For standard choices of 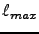 and
and 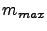 , i.e., both equal
, i.e., both equal 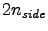 ,
the memory scales as
,
the memory scales as
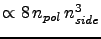 . Thus, for load balanced case the memory per proc is
. Thus, for load balanced case the memory per proc is
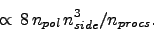
Multiple additional objects of the sizes
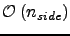 are also stored in memory but are not distributed over the processors.
are also stored in memory but are not distributed over the processors.
- maps -
SCALING
- the routines scales usually well with a number of processors. For the case with no precomputed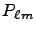 s the scaling is only somewhat
slower than the perfect (
s the scaling is only somewhat
slower than the perfect (
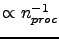 for fixed
for fixed 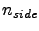 and
and
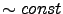 for the fixed theoretical work load, i.e.,
for the fixed theoretical work load, i.e.,
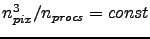 ) up to a rather large number of procs
suggesting that the
communication overhead is indeed small. For the routines
with precomputed
) up to a rather large number of procs
suggesting that the
communication overhead is indeed small. For the routines
with precomputed 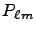 s the decreased number of Flops (due to
the stored
s the decreased number of Flops (due to
the stored 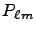 s) makes the scaling flattening out somewhat
earlier.
s) makes the scaling flattening out somewhat
earlier.
RELATIVE PERFORMANCE
- for the standard data distribution over procs, the map2alm routine in general show better load balancing than the alm2map ones. The latter on the other hand scale somewhat better with a number of procs.The unevenness of the load balancing of the alm2map routines is probably due to the map distribution which has not been tuned correctly.
The relative speed of direct and inverse transforms depends on a choice of routines. For the case with no precomputed
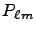 s
as well as with all the
s
as well as with all the 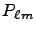 s stored ahead of the run, the direct (map2alm) transforms fare better (cache misses for
alm2map ?!) up to
s stored ahead of the run, the direct (map2alm) transforms fare better (cache misses for
alm2map ?!) up to  . For the case with only scalar
. For the case with only scalar 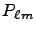 s
precomputed the inverse transform fares a bit (
s
precomputed the inverse transform fares a bit (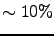 )
better.
)
better.
PERFORMANCE WRT SERIAL HEALPIX ROUTINES (V. 2.01)
- the routines can be used to run on a single processor and their runtimes compares well with those of serial HEALPix routines. The map2alm routines seem to occasionally outperform somewhat the HEALPix ones by around , while the alm2map routines
usually are slower but by not more than
, while the alm2map routines
usually are slower but by not more than . PRECOMPUTING PLM
- precomputation of the scalar is generally beneficial, in particular for the alm2map transforms given a total gain of up to a factor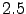 .
The cache
misses do not seem to be the issue, though fewer FLOPS which
need to be performed in that case make the communication overhead
more apparent and at the lower number of processors than in the
case with the "on-the-fly" computation of the
.
The cache
misses do not seem to be the issue, though fewer FLOPS which
need to be performed in that case make the communication overhead
more apparent and at the lower number of processors than in the
case with the "on-the-fly" computation of the 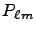 s and the advantage
of the precomputation decreases somewhat for a large number of employed procs.
Given that the extra memory needed to store the
s and the advantage
of the precomputation decreases somewhat for a large number of employed procs.
Given that the extra memory needed to store the 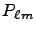 s usually forces
allocating in general more processors the gain from the precomputation may turn out smaller than hoped for.
s usually forces
allocating in general more processors the gain from the precomputation may turn out smaller than hoped for.
Precomputation of all
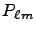 s seems pointless. The memory burden is
really huge and the cache misses (most likely) and the communication overhead result in a significant performance hit, which basically
counterbalances any gains due to the precomputation.
Consequently the relevant routines do not perform any better than
the routines with the "on-the-fly" computation. Clearly not necessarily a
"fundamental" limitation but for sure more work needed here.
s seems pointless. The memory burden is
really huge and the cache misses (most likely) and the communication overhead result in a significant performance hit, which basically
counterbalances any gains due to the precomputation.
Consequently the relevant routines do not perform any better than
the routines with the "on-the-fly" computation. Clearly not necessarily a
"fundamental" limitation but for sure more work needed here.
radek stompor 2007-02-13