Here is an application example of a least square problem resolution which is implemented in test_pcg_mapmat.c . Considering a problem formulated as 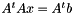 , Solution x can be compute iteratively using conjutgate gradient. Instead computing and storing the whole
, Solution x can be compute iteratively using conjutgate gradient. Instead computing and storing the whole 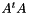 matrix, we apply succesively pointing,
matrix, we apply succesively pointing, 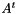 , and unpointing products,
, and unpointing products, 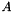 , at each iterate.
, at each iterate.
Classic gradient conjugate algorithm has been slightly modified. As we explain 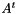 and
and 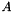 are applied succesively. Furtherwise dotproduct operations in the overlapped domain have been moved in the distributed domain. Espacially we use relation :
are applied succesively. Furtherwise dotproduct operations in the overlapped domain have been moved in the distributed domain. Espacially we use relation : 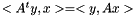 .
.
Algorithm needs into memory 6 vectors :
- 3 in ovelapped domain(x, gradient, direction),
- 3 in distributed domain.
Complexity, counting operations at each iterate, is detailled as follow :
- 4 produits scalaires dans le domaine temporelle (communication = single MPI_Allreduce),
- 3 axpy dans le domaine de la carte (no communication),
- 3 multiplication par
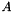 (no communication),
(no communication),
- 1 multiplication par
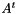 (communication = MIDAPACK Communication scheme).
(communication = MIDAPACK Communication scheme).
double *x, *g, *d;
double *Ax_b, *Ag, *Ad;
MatCreate(&A, m, nnz, MPI_COMM_WORLD);
g = (
double *) malloc(A.
lcount*
sizeof(
double));
d = (
double *) malloc(A.
lcount*
sizeof(
double));
Ax_b = (double *) malloc(m*sizeof(double));
Ad = (double *) malloc(m*sizeof(double));
Ag = (double *) malloc(m*sizeof(double));
for(i=0; i<m; i++)
Ax_b[i] = Ax_b[i]-b[i];
resnew=0.0;
localreduce=0.0;
for(i=0; i<m; i++)
localreduce+=Ax_b[i]*Ad[i];
MPI_Allreduce(&localreduce, &resnew, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
for(k=0; k<KMAX ; k++){
alpha=0.0;
localreduce=0.0;
for(i=0; i<m; i++)
localreduce+=Ad[i]*Ax_b[i];
MPI_Allreduce(&localreduce, &alpha, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
gamma=0.0;
localreduce=0.0;
for(i=0; i<m; i++)
localreduce+=Ad[i]*Ad[i];
MPI_Allreduce(&localreduce, &gamma, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
x[j] = x[j] - (alpha/gamma)* d[j];
for(i=0; i<m; i++)
Ax_b[i] = Ax_b[i]-b[i];
resold=resnew;
resnew=0.0;
localreduce=0.0;
for(i=0; i<m; i++)
localreduce+=Ax_b[i]*Ag[i];
MPI_Allreduce(&localreduce, &resnew, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
beta=0.0;
localreduce=0.0;
for(i=0; i<m; i++)
localreduce+=Ag[i]*Ad[i];
MPI_Allreduce(&localreduce, &beta, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
if(resnew<tol)
break;
d[j]= -g[j] + (beta/gamma)*d[j];
}
More information about pointing operator are detailled, in the pointing function synposis


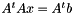 , Solution x can be compute iteratively using conjutgate gradient. Instead computing and storing the whole
, Solution x can be compute iteratively using conjutgate gradient. Instead computing and storing the whole 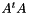 matrix, we apply succesively pointing,
matrix, we apply succesively pointing, 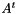 , and unpointing products,
, and unpointing products, 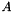 , at each iterate.
, at each iterate.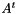 and
and 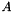 are applied succesively. Furtherwise dotproduct operations in the overlapped domain have been moved in the distributed domain. Espacially we use relation :
are applied succesively. Furtherwise dotproduct operations in the overlapped domain have been moved in the distributed domain. Espacially we use relation : 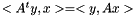 .
.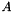 (no communication),
(no communication),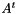 (communication = MIDAPACK Communication scheme).
(communication = MIDAPACK Communication scheme).