MIDAPACK - MIcrowave Data Analysis PACKage  1.1b
Parallel software tools for high performance CMB DA analysis
 All Data Structures Files Functions Variables Typedefs Groups Pages
Data structure and parallelism

Parallel sparse matrix

Considering a matrix 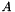$A$, parallelism assume 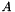$A$ is row-distributed over processes. Each processor has into memory m rows of the global matrix. Reciprocally 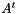$A^t$ is column-distributed, with m columns into memory. That is to say

\[ A = \left( \begin{array}{c}A_0 \\A_1\\ \vdots \\ A_{n_{prc}-1} \end{array} \right) \]

Reciprocally

\[ A^t=(A_0^t, A_1^t, A_2^t, ... A_{n_{prc}-1}^t) \]

.

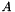As $A$ is a sparse martix, it doesn't store zero values. Furthermore we assume 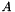$A$ is exactly nnz nonzerovalues. Then building matrix A only require these non-zero values and theirs global columns indices, also called ELL format. Input data consists in two large tab of size m*nnz, where rows are concatenated. This input array have to be passed when calling matrix initializtaion function.

To well ballence the load over processes we have to ensure number of rows time number of non-zero per row is roughly the same on each processor

Input data

The two following examples illustrate the input data needs to build a matrix using MatInit. The first one is a sequential, the second consider 2 processors.

  • sequential case : m=8, nnz=2, indices=[0 1 2 4 0 2 0 2 2 3 3 4 1 4 1 3], values=[1 7 2 8 5 3 5 6 2 9 8 6 1 3 6 4].

    \[ A = \left( \begin{array}{ccccc}1&7&0&0&0\\0&0&2&0&8\\5&0&3&0&0\\5&0&2&0&0\\0&0&2&9&0\\0&0&0&8&6\\0&1&0&0&3\\0&6&0&4&0\end{array} \right) \]

  • parallel case over 2 processors : input data on processor 0 is m=3, nnz=2, indices=[0 1 2 4 0 2 0 2], values=[1 7 2 8 5 3 5 6]. Input data on processor 1 is m=4, nnz=2, indices=[2 3 3 4 1 4 1 3], values=[2 9 8 6 1 3 6 4].

    \[ A = \left( \begin{array}{c} A_0 \\ A_1 \end{array} \right) \]

    \[ A_0 = \left( \begin{array}{ccccc} 1&7&0&0&0\\0&0&2&0&8\\5&0&3&0&0\\5&0&2&0&0\end{array} \right) , A_1 = \left( \begin{array}{ccccc} 0&0&2&9&0\\0&0&0&8&6\\0&1&0&0&3\\0&6&0&4&0\end{array} \right) \]

    Two remarks about the input data structure (ELL format) :
  • it happens that a row has more or less non-zero values that nnz. In this case we can choose the greater nnz and add zero wherever it is necessary with whatever index. For performance we advice to choose an index which has already a value in the row.
  • ELL format is more general than DIA format since non-zero elements of given row do not need to be ordered. Thus permuting non-zero elements of given row in the input data do not change the matrix.

Internal data stucture

The internal structure is more sophisticated than the ELL format. Especially, to enhance matrix operations performance, a precomputation step reshapes the data structure into several arrays : global ordered columns indices, local indices, communication ...

When using MatInit function, precomputation is performed blindly. Nevertheless, for advanced user it is able to initialize a matrix in several steps. This enables to specify differents methods for the precomputations.