MIDAPACK - MIcrowave Data Analysis PACKage  1.1b
Parallel software tools for high performance CMB DA analysis
 All Data Structures Files Functions Variables Typedefs Groups Pages
Communication Algorithm

Transposed matrix vector multiplication is performed in two steps :

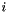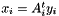  • Firstly, each processor $ i $ multiply a local vector by a local matrix, $ x_i=A_i^t y_i$.
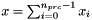
  • Then processors communicated to update the local result vector, $ x = \sum_{i=0}^{n_{prc}-1} x_i $

The second steps involved to communicate and sum elements of all the each local vectors. When size of the problem or number processors increases, this operation may become a bottleneck. To minimize the computationnal cost of this collective reduce operation, Midapack identifies the minimum parts of elements to communicate between processors. Once it is done, collective communication are executed using one of the custommized algorithms as Ring, Butterfly, Nonblocking, Noempty

The communication algorithm is specified when calling MatInit or MatComShape . An integer encodes all the communication algorithms (None=0, Ring=1, Butterfly=2, Nonblocking=3 Noempty=4).