compute_all_xls -
a C-routine for computing auto- and cross- (pseudo) spectra of many maps
Purpose
compute_xls_all computes (pseudo) auto- and cross- spectra given the alm coefficients of multiple maps provided on the input. For N maps there are (N+1)N/2 different spectra, what for even not that large N values may give rise to a significant level of confusion in particular in the paralell environment where both the input and output products are typically distributed over many processors.The main objective of the routine is to facilitate the computation in such cases, while providing an output in an easy to mainpulate and follow format.
> Top of the page
Using compute_xls_all
> Top of the page
Dependencies
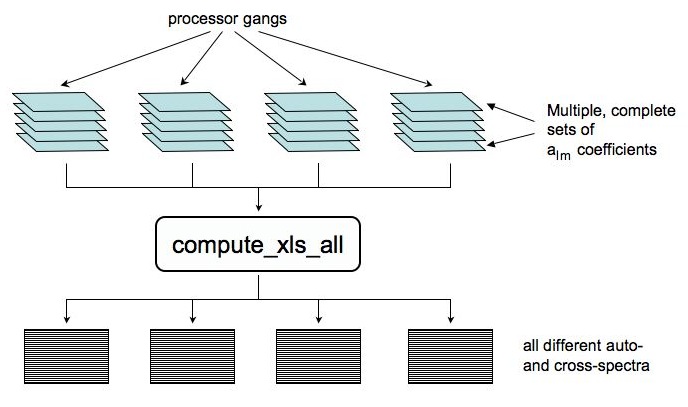
compute_xls_all is coded as an add-on routine to the S2HAT library functionality. It uses and extends functionality of the library routine called collect_xls, which can calculate a basic (cross) spectrum of two sets of alm coefficients stored in the memory of the same processor gang. The routines assumes the data types and layouts, e.g., of the input data (alm tables), as defined by the library. As is the routines requires the S2HAT library (version 2.51 or later) and the FFT, MPI libraries. FFTs are needed by S2HAT, while MPI by both the routine and S2HAT.In a typical application envisaged here, see e.g., Fig 1. below, the S2HAT routines of the map2alm type are first used by many processors subset (called hereafter gangs) all working in parallel and each producing the alm coefficients from multiple maps as stored in each gang memory.. The compute_xls_all routine can be used then to seamlessly compute all the auto- and cross- spectra of all the alm sets as pre-computed by all gangs.
The role of the routine is to provide a simple interface to mask the actual messiness of the multiple communication and data distribution complexity, which unavoidably arise in such cases.
> back
Calling sequence
s2hat_int4 compute_all_xls ()
INPUT
- nxtype == ncomp -- only same component-spectra are computed;
- nxtype == ncomp+2 ( ncomp>1) -- all ncomp same-component spectra and one different-component spectrum (e.g., T1E2 and E1T2 if ncomp == 3) are computed;
- nxtype == ncomp^2 (ncomp > 1) -- all same-component and all different-component spectra are computed.
OUTPUT
(nlmax+1)*nxtype*(nxspec*nmaps^2-((nmaps-1)*nmaps)/2),
where
- nxspec = (n_gangs+1)/2 - if n_gangs odd,
- nxspec = n_gangs/2+1 - n_gangs even and igang < n_gangs/2,
- nxspec = n_gangs/2 - n_gangs even and igang >= n_gangs/2.
(See Section on Communication patterns for more explanations.)
The vector xcl is organized in a way that nxtype spectra for each pair of maps are concatenated together and are followed by the spectra for another pair. The pairs of the maps for each part of the xcl vector are identified by the data sets global id numbers stored in the frstSpec and scndSpec.
(nxspec*nmaps^2-((nmaps-1)*nmaps)/2),
which store the global numbers of the data sets (first and second of the pair) used for spectra computations.
See Section on Communication patterns for more explanations.
> back
Input/Output
On the input the routine expect multiple sets of the alm coefficients (each corresponding to a map), spectra of which need to be computed. All the processors used to run the parallel job are conceptually divided into gangs, each containing the same number of processors. Those are defined by the input parameters n_gangs and gangSize, respectively. Both these number can be arbitrary though non-zero and the latter has to be the same for all gangs.Each gang is pressumed to store some number of complete sets of alm coefficients. The coefficients are assumed to be distributed over the processors of the gang as defined by the standards of the S2HAT library. The number of complete sets of the coefficients is assumed to be the same for each gang. It is given by the input parameter nmaps.
On the output the routine will provide all the different (pseudo) spectra computed from the input alm coefficients. The spectra are divided into subsets, as many as the gangs, each containing some number of complete spectra and which are stored, non-distributed, in the memory of the 0th proc of each gang. Which spectra are stored where is discussed in the Communication section below. However, for every spectrum the routine provides the global number of the two sets of alms which were used for its calculations. Those are stored in the frstSpec and scndSpec vectors, so that ith spectrum on a given gang is computed from frstSpec[i] and scndSpec[i] sets of alms. The global numbering scheme of the input data sets is such that a set stored by the gang igang as iset has a global number given by
global set number := igang nmaps + iset.
This allows for an easy identification of the output spectra.
Note that the sets of alm coefficients can have multiple components, e.g., they can have two components, E and B, for the non-zero spin maps, or have 3 components corresponding to T, E, and B, for typical polarized map set containing three Stokes parameter maps, I, Q, U. In such cases what spectra of these components are computed is defined by the input parameter nxtype. However, all such "internal" spectra will be stored by the same gang as defined by the global number of the appropriate input set. The data flow for the routine is shown in the figure below.
> back
Communication patterns
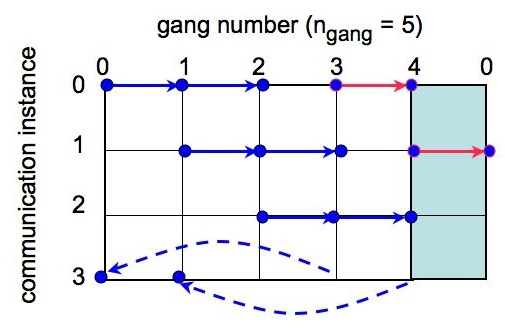
The main challenge in calculating efficiently all the spectra, given the precomputed alm coefficients, is the need for efficient communication pattern, as the required calculations at some point involve the data stored in the memory of any pair of the gangs. The compute_xls_all routine works for any number of gangs. For a single set of alm coefficients per gang it performs (n_gangs+1)/2 + 1 simultaneous communications out of which (n_gangs+1)/2 are the two (or exceptionally one if n_gangs is odd) MPI_Bcasts calls performed simultaneously as involving dosjoint subsets of all gangs. The last communication instance involves MPI_Send and MPI_Recv communications performed between disjoint (n_gangs+1)/2 pairs of gangs. These communication instances are shown in Fig. 2.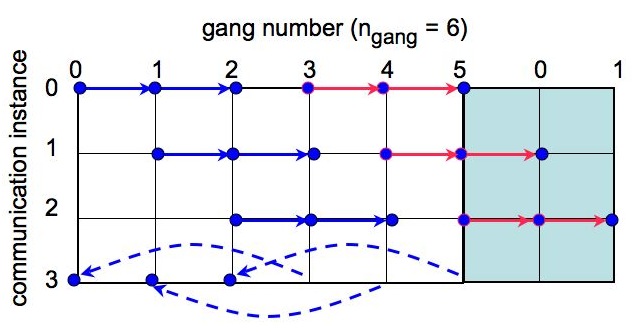
|
We note that for a communication instance, ic, the gangs with numbers, igang, such that
(igang - ic+n_gangs)%n_gangs < (n_gangs+1)/2
participate always in the first (marked in blue in Fig. 2) MPI_Bcast while all the others - in the second call (red) with an exception of the last broadcasts, when for the odd number of gangs the second call does not happen. This provides an easy way to separate all the gangs into two groups each communicating only internally. Consequently, there is always n_gangs broadcasts performed by the code for each of the nmaps maps. These are arranged in (n_gangs+1)/2 communication instances.
We also note that broadcasting gangs are always the ones for which either,
igang = ic
or
igang = ic + (n_gangs+1)/2.
On the MPI_Send/Recv stage the sending gangs are the ones for which
igang > (n_gangs+1)/2
and respective receiving ones are the one with number jgang
jgang = igang - (n_gangs+1)/2.
We note therefore that all the gangs with igang < (n_gangs+1)/2 receive the data then, and that igang = (n_gangs+1)/2 does that only if n_gangs is even. Otherwise it remains idle.
Alltogehter there is n_gangs/2 MPI_Send/Recv process for each of nmaps alm sets.
The direction of MPI_Send/Recv can be clearly inverted with no change in what spectra are at the end computed, however the one proposed here leads to a better (or in fact as good as only possible) output data balance and it is therefore preferred here.
After each instance of the communication, each gang which received new set of alms computes its (cross)spectrum with the data set(s) stored permanently in its memory. The (cross) spectra are computed using the S2HAT routine compute_xls. Once the spectra are calculated the temporary memory needed to accomodate the received spectra is reused for the next data set, while the spectra are preserved in the memory of the gang_root processor of each gangs. In this way the extra memory needed by each gang is equal to that needed to store one extra data sets plus whatever it is needed to store all the calculated spectra.
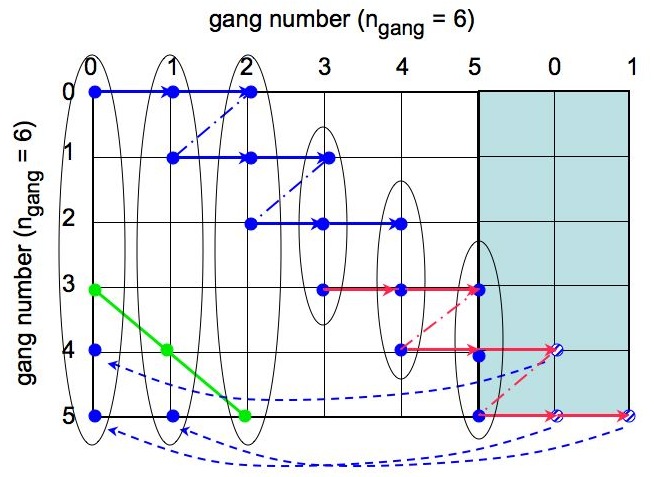
The ordered in which the spectra are calculated and stored is illustrated in Fig. 3 below. The figure also shows how the spectra are assigned to the gangs, which compute and store them.
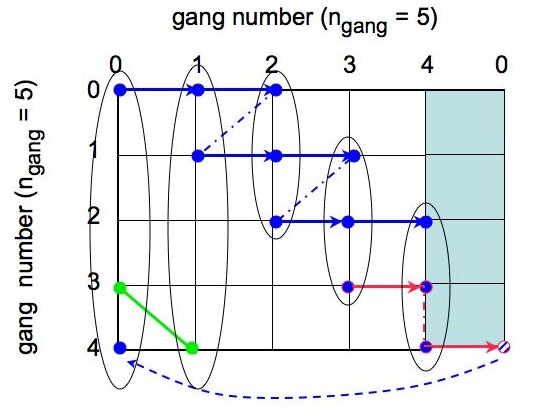
|
If there are multiple alm sets on the input, nmaps != 1 , then the routine performs the entire communication sequence nmaps times rather then perform the same number of communications as in nmaps=1 case but with higher volume of the transfered data. Though the choice implemented in the routine could impact the code performace if the communication latency is unusually long, in practice, unless the input data are distributed extremely finely (meaning typically that there are too many processors in the gang given the size of the alm sets), this does not seem to cause any problem, while sending the large data volumes as implied by the second approach outlined above at least in principle could.
For a single data set per gang, nmaps == 1, if n_gangs is odd each gang with a number, igang, participates in
(n_gangs/2) MPI_Bcasts if igang < (n_gangs+1)/2
and
(n_gangs+1)/2 (= n_gangs/2+1) MPI_Bcasts if igang >= (n_gangs+1)/2.
(This is because of the one missing broadcast in the last broadcasting instance (Fig. 2). However, the MPI_Send/Recvd calls will send one more alm set to each of the former gangs. As a result each gang will have the same number of spectra stored at the end equal to
nxspec = (n_gangs+1)/2 - if n_gangs odd.
For even n_gangs each gang participates in the same number of broadcasts, receiving the same number of data sets equal to,
n_gangs/2.
Then the following send and receives add one more data set and thus spectrum to the first n_gangs/2-1 gangs. Consequently,
nxspec = n_gangs/2+1 - n_gangs even and igang < n_gangs/2,
nxspec = n_gangs/2 - n_gangs even and igang >= n_gangs/2.
Whenever nmaps != 1 let us first assume that all other gangs but the selected one has just one data set. Then the selected gang will receive nxspec data sets as calculated above and compute its spectra with the nmaps data sets stored by the selected gang. This will in general result in nmaps nxspec spectra. Therefore for all the nmaps data sets stored in the memory of all the other gangs we get nmaps^2 nxspec. Now one should observe that for each gang one of the broadcasts really sends the data set to the same gang. For this specific case there is only ((nmaps+1) nmaps)/2 different spectra rather than nmaps^2, we therefore need to subract the duplicates from the total count of the spectra. We thus arrive at,
nmaps^2 nxspec - ((nmaps-1)nmaps)/2
as the final number of spectra stored in the memory of each gang. Here nxspec is as computed above and thus potentially different for different gangs. We note that the number of spectra per gang depends on the square of nmaps but only linearly on n_gangs so for the fixed number of the all the maps to be processed it can be decreased by using more gangs and cutting on nmaps. Summing the above expression over gangs we obtain the total number of computed and stored spectra to be,
((n_gangs nmaps +1)n_gangs nmaps)/2,
which is equal to all the different spectra which can be computed from n_gangs nmaps input data sets.
> back
Memory consideration
The total memory allocated by compute_xls_all internally, i.e., in addition to the memory needed to store the input and outputs - which needs to be allocated by the master code before calling the routine, is equal to the memory needed to store one extra data set by each gang of processors used for the calculation. Typically the memory consumption of the routine is dominated by the data sets therefore if we process nmaps data sets simultaneously the extra memory overhead is at most 1/nmaps fraction of the total memory needed for to store the inputs. The memory per processor, which is needed to store the data sets (input and the internally allcoated one), will depend on a size of the gang, and can be decreased by defining the gangs appropriately large. The memory per gang needed to store the output spectra is given by(nxspec*nmaps^2 - ((nmaps-1)nmaps)/2) x nxtype x (nlmax+1) x sizeof( double).
Here the first factor is the number of spectra stored by each gang, nxtype defines how many spectra are computed for a pair of two maps (those can be multi component maps) and nlmax is the maximum number of the multipole to be computed. We note that all the spectra are stored in the memory of a gang_root processor of each gang, which therefore has to have sufficient memory size. In fact this could be easily improved if needed, however for time being this limitation can be bypassed by using more gangs and decreasing a number of maps, nmaps, per gang.
> back
> Top of the page
Download
> Top of the page
Acknowledgments, etc
This routine has been coded, tested, and debugged (or at least it seems so) by R. Stompor and M. Tristram.We acknowledge partial support of French National Research Agency (ANR) through COSINUS program (project MIDAS no. ANR-09-COSI-009).
> Top of the page
Contact
radek(at)apc(dot)univ(dash)paris7(dot)fr
> Top of the page > Home

|
Centre National de la Recherche Scientifique Laboratoire Astroparticule et Cosmologie Equipe de Traitement des Données et Simulations (ADAMIS) |

|
Contact: Radek Stompor (radek(at)apc(dot)univ(dash)paris7(dot)fr) © 2007 rs |